2025年04月24日成考专升本每日一练《高等数学一》

2025年成考专升本每日一练《高等数学一》4月24日专为备考2025年高等数学一考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、＝（）。

• A：3
• B：2
• C：1
• D：0

答 案：C

解 析：x²＋1在（-∞，∞）都是连续的，函数在连续区间的极限，可直接代入求得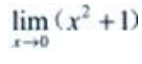，＝0＋1＝1。

2、下列函数中在点x₀＝0处可导的是（）。

• A：
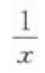
• B：|x|
• C：
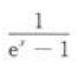
• D：|x|²

答 案：D

解 析：AC两项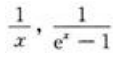，在x₀＝0处无定义不可导；B项，在x₀＝0处有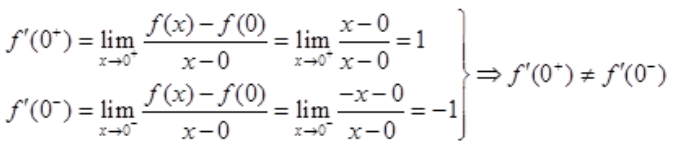所以该函数在x₀＝0处不可导；D项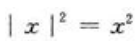，，显然在x₀＝0处可导。

3、微分方程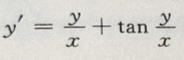的通解为（）

• A：
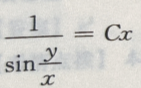
• B：
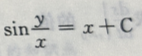
• C：
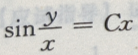
• D：

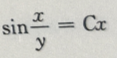
答 案：C

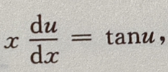解 析：设代入有所以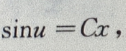原方程的通解为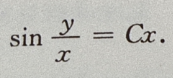

主观题

1、设e^x＋x＝e^y＋y，求。

答 案：解：对等式两边同时微分，得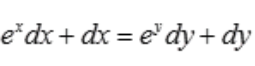，故。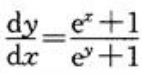

2、设f（x，y）为连续函数，交换二次积分的积分次序。

答 案：解：由题设知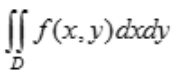中积分区域的图形应满足1≤x≤e，0≤y≤lnx，因此积分区域的图形见下图中阴影部分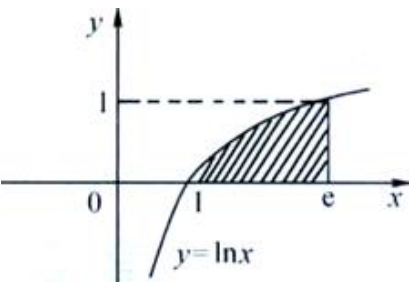．由y＝lnx，有x＝e^y。所以。

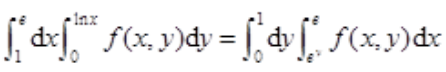3、求过点M₀（0，2，4），且与两个平面π1，π2都平行的直线方程，其中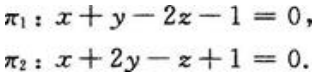

答 案：解：如果直线l平行于π1，则平面π1的法线向量n1必定垂直于直线l的方向向量s．同理，直线l平行于π2，则平面π2的法线向量n2必定满足n2⊥s．由向量积的定义可知，取由于直线l过点M₀（0，2，4），由直线的标准方程可知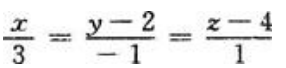为所求直线方程。

填空题

1、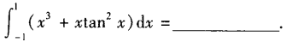  

答 案：0

解 析：本题考查的知识点为定积分的性质。  

2、设3x³为f(x)的一个原函数，则f(x)＝（）。

答 案：9x²

解 析：由题意知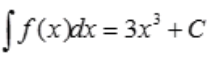，故。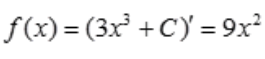

3、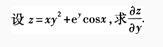  

答 案：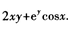

解 析：

简答题

1、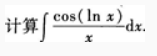  

答 案：