2025年04月25日成考高起点每日一练《数学(文史)》

2025年成考高起点每日一练《数学(文史)》4月25日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、一批产品共有5件，其中4件为正品，1件为次品，从中一次取出2件均为正品的概率为（）。

• A：0.6
• B：0.5
• C：0.4
• D：0.3

答 案：A

解 析：本题主要考查的知识点为随机事件的概率。 一次取出2件均为正品的概率为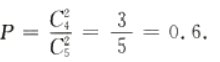

2、下列函数中，为奇函数的是（）。

• A：y=log3^x
• B：y=3^x
• C：y=3x²
• D：y=3sinx

答 案：D

3、函数y=cos⁴x-sin⁴x（x∈R）的最小正周期为（）。

• A：
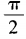
• B：π
• C：2π
• D：4π

答 案：B

解 析：y=（cos²x+sin²x）（cos²x-sin²x）=cos2x， 所以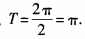

4、已知等比数列a₁=1，a₉=25，则a₅=（）。

• A：25
• B：-5
• C：±5
• D：5

答 案：C

主观题

1、求函数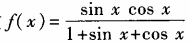（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

2、已知等差数列前n项和 （Ⅰ）求通项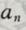的表达式 （Ⅱ）求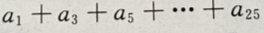的值  

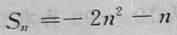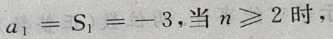
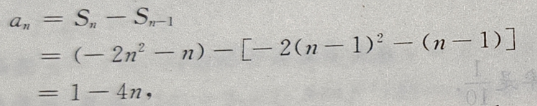
答 案：（Ⅰ）当n=1时，由得 也满足上式，故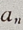=1-4n（n≥1） （Ⅱ）由于数列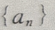是首项为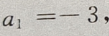公差为d=-4的等差数列，所以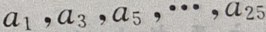是首项为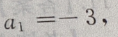公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：  

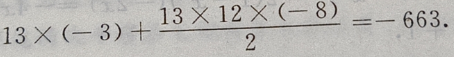
3、若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围

答 案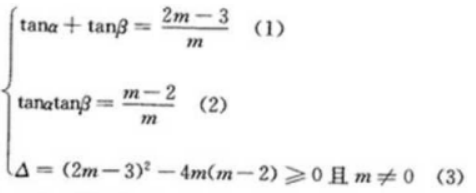： 由(1)(2)得，tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞，-3/2)U(-3/2，3/4)  

4、已知a^m=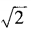，aⁿ=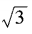，求a^3n-4m的值。  

答 案：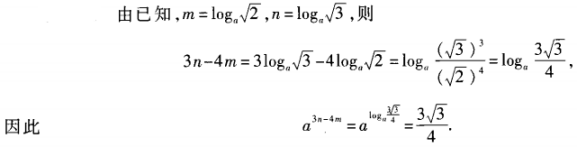

填空题

1、“a＞b”是“a-c＞b-c”的______。

答 案：充要条件

2、设直线y=2x+m与抛物线y²=4x没有公共点，则m的取值范围是______。  

答 案：