2025年04月27日成考高起点每日一练《数学(理)》

2025年成考高起点每日一练《数学(理)》4月27日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）

• A：以A为直角的三角形
• B：b=c的等腰三角形
• C：等边三角形
• D：钝角三角形

答 案：B

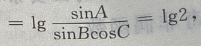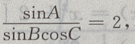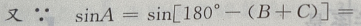
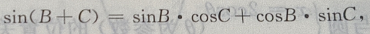
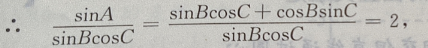
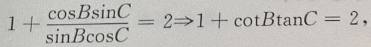
解 析：判断三角形的形状，条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2，由对数运算法则可得,左 两个对数底数相等则真数相等：即2sinBcosC=sinA 在△ABC中，∵A+B+C=180°，∴A=180°-（B+C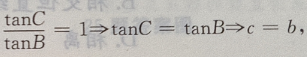）, 故为等腰三角形

2、设集合M={1,2,4}，N={2,3,5}，则集合M∪N=（）.

• A：{2}
• B：{1，2，3，4，5}
• C：{3，5}
• D：{1，4}

答 案：B

解 析：M∪N={1,2,4}∪{2,3,5)= {1，2，3，4，5} (答案为B)

3、已知α∩β=a，b⊥β，b在α内的射影是b’，那么b'和α的关系是（）

• A：b'//α
• B：b'⊥α
• C：b'与α是异面直线
• D：b'与α相交成锐角

答 案：B

解 析： ∴由三垂线定理的逆定理知,b在α内的射影b'⊥α，故选B  

4、曲线y＝x³＋2x－1在点M（1，2）处的切线方程是（）。

• A：5x－y－3＝0
• B：x－5y－3＝0
• C：5x＋y－3＝0
• D：x＋5y－3＝0

答 案：A

解 析：由于y’=3x+2,所以曲线y=x³+2x-1在点 M(1,2)处的切线的斜率是y’|_x-1=5.所求曲线的切线方程是y-2=5(x-1),即5x-y-3=0.(答案为A)

主观题

1、已知关于x的二次方程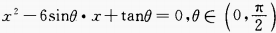的两根相等，求sinθ+cosθ的值。

答 案：

2、已知等差数列前n项和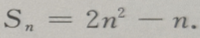 （Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和

答 案：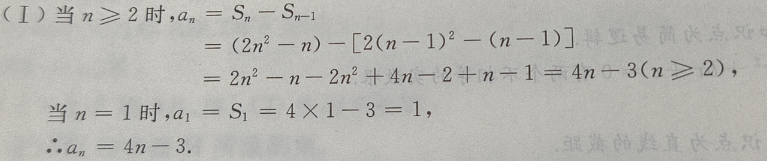  

3、设（0＜α＜π），求tanα的值。

答 案：

4、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得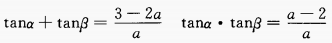

填空题

1、若A（3，a），B（-4，3）两点间的距离为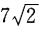，则a=______。

答 案：a=-4或10

解 析：由两点间的距离公式得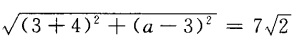，，两边平方整理得（a-3）²=7²→a-3=±7→a=-4或10。

2、化简sin（x+y）-2cosxsiny=______.  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）