2025年05月27日成考专升本每日一练《高等数学二》
成考(专升本) 2025-05-27作者:匿名 来源:本站整理
2025年成考专升本每日一练《高等数学二》5月27日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、设函数z=xe2y,则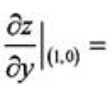 ().
().
- A:0
- B:
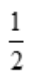
- C:1
- D:2
答 案:D
解 析: ,则
,则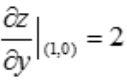 .
.
2、设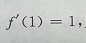 则
则 等于()
等于()
- A:0
- B:1
- C:1/2
- D:2
答 案:C
解 析:因 于是
于是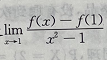
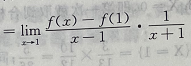
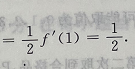
主观题
1、加工某零件需经两道工序,若每道工序的次品率分别为0.02与0.03,加工的工序互不影响,求此加工的零件是次品的概率.
答 案:解:A={第一道工序是次品),B={第二道工序是次品),C={产品是次品},则C=A+B且A与B相互独立,P(C)=P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)·P(B)=0.02+0.03-0.02×0.03=0.0494.
2、袋中有4张卡片,上面分别写有从1~4四个整数.让甲乙两人各自从中挑选一张,甲先挑选:选完后卡片不放回,同时再放入一张写有数字5的卡片,接下来让乙去挑选.记乙挑得的数字为X.试求随机变量X的概率分布,并求数学期望E(X).
答 案:解:(1)随机变量X的可能取值为1,2,3,4,5.显然P(X=1)=P(X=2)=P(X=3)=P(X=4),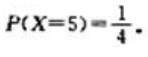 设事件A为甲挑到写有数字1的卡片,则
设事件A为甲挑到写有数字1的卡片,则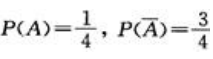 .
.
事件B为乙挑到写有数字1的卡片,则P(B)=P(X=1),因此
易知P(B|A)=0,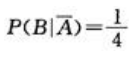 ,因此
,因此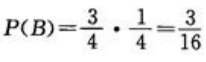 .
.
所以离散型随机变量X的概率分布为:
(2)
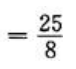 .
.
填空题
1、设函数 ,在x=0处连续,则a=().
,在x=0处连续,则a=().
答 案:2
解 析:因为函数在x=0处连续,故有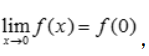 由于
由于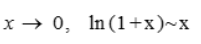
 所以a=2.
所以a=2.
2、设z=f(x²+y²),则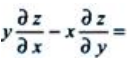 ()
()
答 案:0
解 析:设u=x2+y2,则z=f(u)。
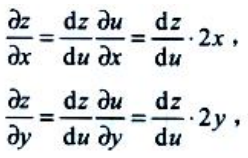
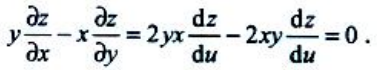
简答题
1、已知某篮球运动员每次投篮投中的概率为0.9,记X为他两次独立投篮投中的次数。①求X的概率分布;
②求X的数学期望。
答 案:①设Ai=“第i次投篮投中”(i=1,2),则两次独立投篮投中的次数X的可能取值为0,1,2。 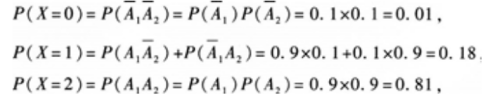 从而X的概率分布为:
从而X的概率分布为:
②E(X)=0×0.01+1×0.18+2x0.81=1.80
2、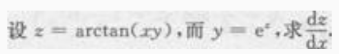
答 案: