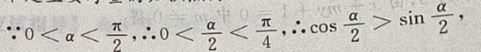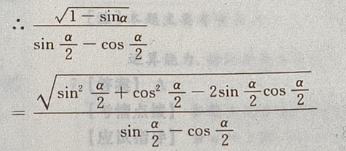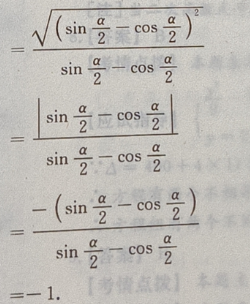2025年05月27日成考高起点每日一练《数学(文史)》

2025年成考高起点每日一练《数学(文史)》5月27日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设集合 （）。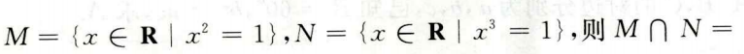

• A：{1}
• B：{-1}
• C：{—1，1）
• D：

答 案：A

解 析：本题主要考查的知识点为集合的运算。 由题意M={-1，1}，N={1}，所以M∩N=（1}。  

2、设f（x）=x³+4x²+11x+7，则f（x+1）=（）。

• A：x³+7x²+22x+23
• B：x³—7x²+22x+23
• C：x³+7x²-22x+23
• D：x³-7x²-22x+23

答 案：A

解 析：f(x+1) =(x+1)³ +4(x+1}²+11(x+1)+7 =x³+3x²+3x+1+4x²+8x+4+11x+11+7 =x³+7x²+22x+23 综上所述，答案:x³+7x²+22x+23

3、已知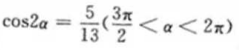,则tanα等于（）。

• A：2/3
• B：3/2
• C：-3/2
• D：-2/3

答 案：D

解 析：

4、已知2^a=3，2^b=6，2^C=12，则（）。

• A：b²=a+c
• B：2b=ac
• C：2b=a+c
• D：b²=ac

答 案：C

解 析：由已知，2^a·2^c=36，即2^a+c=36。又（2^b）²=6²，2^2b=36，则2^2b=2^a+c，2b=a+c选C。

主观题

1、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：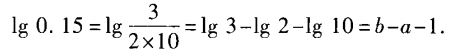

2、教室里有50人在开会，其中学生35人，家长12人，老师3人，现校长在门外听到有人在发言，那么发言人是老师或学生的概率为多少？  

答 案：此题属于互斥事件，发言人是老师的概率为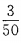，是学生的概率为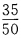，故所求概率为。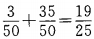

3、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。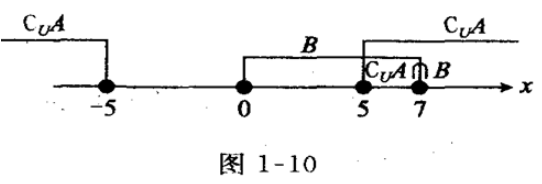

4、设函数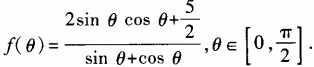 （1）求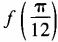；（2）求函数f（θ）最小值。

答 案：

填空题

1、log₂[log₂（log₃81）]=______。  

答 案：1

解 析：由于log₃81=log₃3⁴=4，于是 原式=log₂（log₂4）=log₂2=1。  

2、设则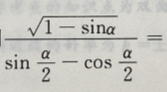

答 案：-1

解 析：