2025年05月28日成考高起点每日一练《数学(文史)》

2025年成考高起点每日一练《数学(文史)》5月28日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知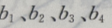成等差数列，且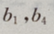为方程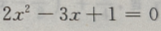的两个根，则的值为（）  

• A：
• B：
• C：
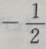
• D：

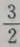
答 案：D

解 析：由根与系数的关系得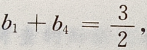由等差数列的性质得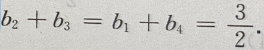

2、掷两颗骰子点数之和等于4的概率是（）。

• A：
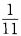
• B：
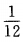
• C：
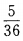
• D：

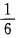
答 案：B

解 析：掷一对骰子的等可能结果共有n=36种，点数之和等于4的结果有1+3=4，3+1=4，2+2=4，故有m=3种，所以其概率为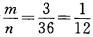故选B。  

3、已知α为三角形的一个内角，且sinα+cosα=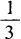则α∈（）。

• A：
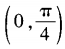
• B：
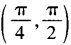
• C：
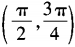
• D：

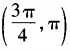
答 案：C

解 析：由已知得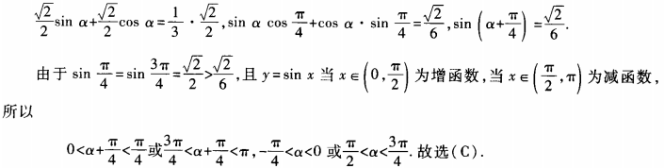  

4、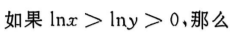

• A：
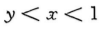
• B：
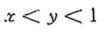
• C：
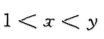
• D：

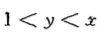
答 案：D

解 析：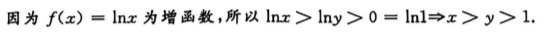

主观题

1、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为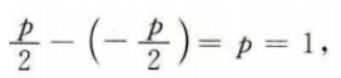 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=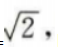因此A点坐标为 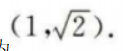设B点坐标为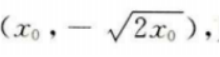

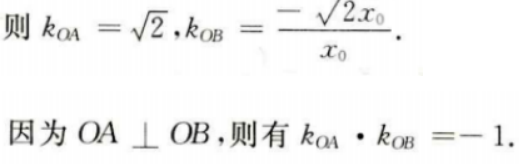
2、已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三边之长。  

答 案：三角形的三边边长分别为4，5，6。

3、

答 案：

解 析：

4、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

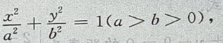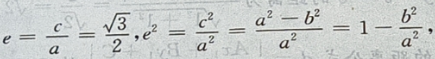
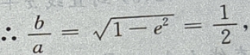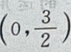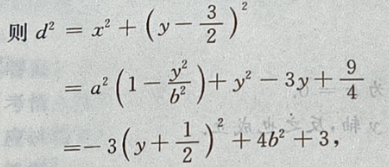
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 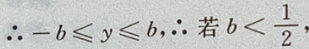则在y=-b时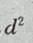，最大，即d也最大。  

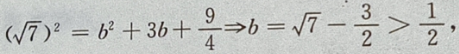
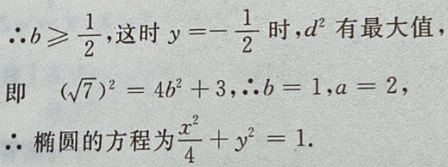
填空题

1、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45

2、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。  

答 案：85  

解 析：本题主要考查的知识点为中位数. 将成绩按由小到大排列：63，77，79，81，85，88，89，94，99.因此中位数为85。