2025年05月28日高职单招每日一练《数学(中职)》

2025年高职单招每日一练《数学(中职)》5月28日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、在一次歌手大赛上，七位评委为某歌手打出的分数为9.4,8.4,9.4,9.9,9.6,9.4,9.7.去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为()  

• A：9.4,0.484
• B：9.4,0.016
• C：9.5,0.04
• D：9.5,0.016

答 案：D

解 析：去掉一个最高分和一个最低分后，剩余数据9.4,9.4,9.6,9.4,9.7的平均值为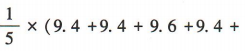9.7)=9.5,方差为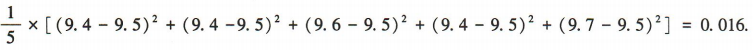

2、设F₁,F₂是双曲线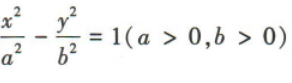的两个焦点，B是虚轴的一个端点.若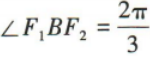则该双曲线的渐近线方程为()

• A：y=±2x
• B：y=±√2x
• C：
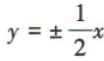
• D：

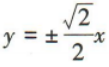
答 案：D

解 析：设双曲线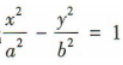的焦距为2c,则左、右焦点的坐标分别为F₁(-c,0),F₂(c,0).不妨设虚轴的一个端点B的坐标为(0,b).由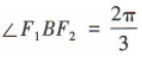及双曲线的对称性可得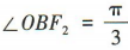(O为坐标原点),所以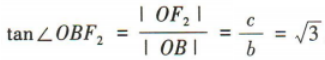,所以c=√3b,所以a=√c²-b²=√2b,所以双曲线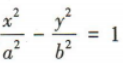的渐近线方程为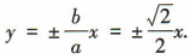

3、在△ABC中，内角A,B,C所对的边分别为a,b,c.已知a=6,,A=30°,则c=（）

• A：6
• B：12
• C：6或12
• D：

答 案：C

解 析：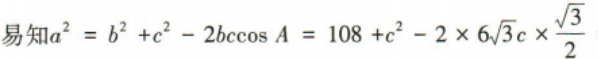

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、在二项式(x-1)⁶的展开式中,系数最小的项是第()项.  

答 案：4

解 析：易知(x-1)⁶的展开式的通项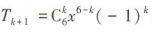,所以当k取1,3,5时,系数小于0.由组合数的性质知当日仅当k=3时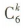，取最大值,所以当k=3时,系数取最小值,所以系数最小的项是第4项.

2、已知{an}是首项a₁=1.公差d=3的等差数列，若a_n=2005.则n等于（）  

答 案：669

解 析：因为等差数列{a_n}的首项a₁=1,公差d=3,所以a_n=1+3(n-1)=3n-2,由3n-2=2005可得n=669.

3、在△ABC中，内角A,B,C的对边分别为a,b,c,且a=3,b=2,A=60°. (1)求sinB; (2)求△ABC的面积

答 案：

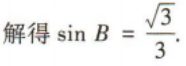
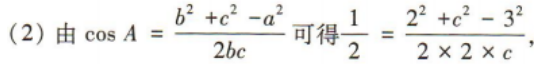
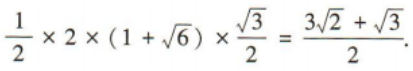
简答题

1、已知函数f(x)=x²+2ax+2,x∈[-5,5]. (1)当a=-1时，求函数f(x)的最大值和最小值； (2)若f(x)在区间[-5,5]上是单调函数，求实数a的取值范围

答 案：(1)当a=-1时，f(x)=x²-2x+2=(x-1)²+1, 所以在区间[-5,5]上，当x=1时，函数f(x)取得最小值，为f(1)=1, 当x=-5时，函数f(x)取得最大值，为f(-5)=37 (2)f(x)=x²+2ax+2=(x+a)²+2-a². 若f(x)在区间[-5,5]上是单调函数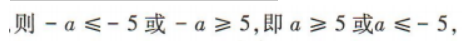， 故实数a的取值范围为(-∞,-5]∪[5,+∞).